DCSG: a discussion on geometry
As we were discussing in the welcome forum, one of the most important aspects of a cable is geometry. While on the surface it may seem like a minor or even superfluous detail, geometry plays a major role in the efficacy of a cables ability to transmit signal from point A to point B. There are many factors that influence a cables ability to transfer signal. Among them, conductivity of the conductor, electromagnetic shielding, radio frequency shielding, inductance, impedance and multitude other factors.
Particularly prominent in modern life is radio frequency interference and other electromagnetic interferences. With the huge spike in local devices that operate by blasting radio frequencies in all directions, proper shielding from RF is an absolute must in a cable. The solution to this seems obvious on the surface; shielding. Just cover the cable with foils and braided materials specifically designed to mitigate this issue. The problem with this solution is that shielding is often implemented improperly. For example, conductors are haphazardly wrapped with foils that are in direct contact with its dielectric. Similar to a guitar string sympathetically vibrating when another string is plucked, conductors that are in close proximity with other metal with ferromagnetic (and/or paramagnetic) properites will lose some of its energy to adjacent materials while transferring signal. I refer to this as inductive thievery. It is one of the leading causes of the loss of vibrance within the signal conductor. Nuance is lost, dynamics are dulled and that subjective ‘emotion’ is stripped away.
 inside a star quad cable, note the close proximity of the signal conductors to adjacent ground/common as well as proximal shielding layer, all of which rob the signal cable of vibrance, nuance, and neutrality.
inside a star quad cable, note the close proximity of the signal conductors to adjacent ground/common as well as proximal shielding layer, all of which rob the signal cable of vibrance, nuance, and neutrality.There are better ways of protecting a signal from such losses. One of the most effective is a simple ’twist’ to the cabling. Twisting a cable adds a chirality to the EM field that is induced by the signal. Rather than ‘shielding’ a cable, twisting a cable rejects noise by virtue of this chiral directionality (either chiral left or chiral right). One of the most effective twisted geometry cables is Star Quad configuration. 4 conductors, two for signal, two for common/ground arranged where the signal conductors are opposite of each other and same with the common/ground cables. (See diagram) Star quad is very effective and works decently well over distances. However, as with a shield, star quad suffers from inductive loss via the proximity of the ground/common cable to the signal cable. There is very little spacing between conductors and thus we run into the the same issues of inductive thievery. The result is phase and frequency smear that translates into muddied midrange, astringent highs (as is particularly the case with silver) and bloating in bass.
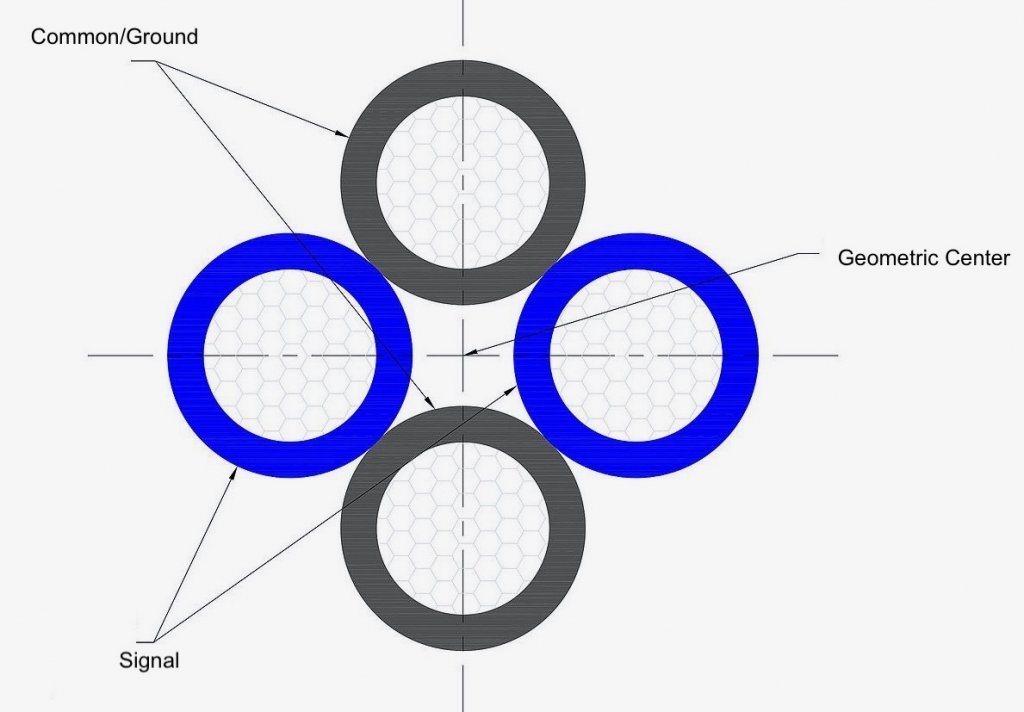 A cross section of a basic star quad configuration. Again, note the close proximity of all conductors.
A cross section of a basic star quad configuration. Again, note the close proximity of all conductors.So, the question becomes how do we take advantage of star quad geometry's strengths while simultaneously mitigating some of the issues with the design? This is a problem that requires an almost complete re-engineering. First, I addressed the issue of conductor spacing that star quad suffers. By spacing the conductors away from each other while maintaining the chiral twisting inherent in star quad I was able to drastically lower inductive thievery. Next, I inserted a nylon spacer in the center of the geometry to prevent the interior of the twist from coming within close proximity to the other conductors. These solutions eliminate inductive loss issues between common/ground and signal.
Lower strand count:One of the central philosophies of my designs is a low strand count per bundle. This helps eliminate strand interaction that plagues most high strand count cables. By lowering the strand count to 10 or less strands of .08mm diameter (as thin as a human hair) per bundle, there is a dramatic drop in strand interaction. Reducing strand interaction has the effect of giving the cable a much more neutral sound regardless of the material. And by having such thin stranding, skin effect is reduced to a minimum. While all of this drastically improves sound quality, the unintended consequence of a low strand count per bundle, is a mere 4 bundle with 8-10 strands of ultra thin wire is insufficient to transfer signal appropriately. So I found I had inadvertently engineered myself into a corner, I needed a new solution.

 Not just a purdy face, DCSG rejects noise and prevents crosstalk between leads.
Not just a purdy face, DCSG rejects noise and prevents crosstalk between leads.Rather than just a right handed or left handed twist, Hapa Analog cables utilize both left and right handed twisting, inducing a field in both left handed and right handed directions, lending an even
higher degree of RFI/EMI rejection. This solution also delivers twice the number of leads without compromising any other aspect of the design philosophy, all leads are spaced away from each other and any leads that cross paths, do so at a 90 degree angle, thus reducing crosstalk to a statistical minimum. As an added bonus, the aforementioned issue of low strand count is easily solved with DCSG delivering twice the number of leads, 8 in total.
Thanks for reading!This is the meat and potatoes of Dual Chirality Star Geometry or DCSG for short. Pristine signal transfer, low strand count per bundle, drastically reduced inductive thievery, and superior RFI/EMI rejection. I threw every design solution I had at DCSG, if you are interested in learning more about Hapa's tech, take a look at our
tech section Most of Hapa Audio analog cables utilize DCSG to great effect. Being handmade, DCSG is a beast of an undertaking and requires a high level of precision, attention to detail, and patience! I think the end result is well worth the effort and I invite you all to experience it in your setup.